컴퓨터의 소숫점 문제

• 기본적으로 구조상 소숫점 계산을 잘 못합니다. 이렇게 말씀드리면 어떤 분께서는 "엥 무슨소리야 절대 그렇지 않은데 당장 자바에서 혹은 내가 쓰는 언어에서는 정확하게 잘만되던데?"라고 생각하실 수 있습니다. 오늘은 이 이야기를 제가 알고 있는 선에서 자세히 풀어나가보자 합니다.
• 우선 앞에서 얘기했던 "어떤 분"의 주장을 한번 더 자세히 들어보겠습니다. "자바dp 0.1 + 0.2 해보세요. 심지어 double 보다 더 적은 bit 수를 쓰는 float 를 써도 잘만됩니다. 보세요"
• public class MyFloat {
   public static void main(String... args) {
     float a = 0.1f;
     float b = 0.2f;
     
     System.out.println("result = ", a+b)
  }
  }
  ​
  // CONSOLE
  // result = 0.3
• 맞습니다. 결과가 0.3 이 나왔습니다. 하지만 다른 언어도 한번 살펴볼까요? 우선 파이썬 그다음 자바스크립트를 한번 살펴보겠습니다.

  a = 0.1
  b = 0.2
  console.log(`result = ${a+b}`)
  ​
  // CONSOLE
  // result = 0.30000000000000004

• # PYTHON3
  ​
  a = 0.1
  b = 0.2
  print(f"result = {a+b}")
  ​
  # CONSOLE
  # result = 0.30000000000000004
• 이렇게 된 이유는 무엇일까요? 자바는 위의 둘 언어보다 더 뛰어난 언어여서 더 높은 정확도를 지니는 걸까요? 오해를 하실 수도 있을거 같아 자바의 코드를 일부 변형해 보겠습니다.
• public class MyFloat {
   public static void main(String... args) {
     float a = 0.1f;
     float b = 0.2f;
     
     System.out.println("float result = "+String.format("%.17f",a+b));
     
     double c = 0.1;
     double d = 0.2;
     
     System.out.println("double result = "+String.format("%.17f",c+d));
  }
  }
  ​
  // CONSOLE
  // float result = 0.30000001192092896
  // double result = 0.30000000000000004
• 여기서 코드의 변경점은 double 변수(c, d)를 추가했다는 것이고 소수 17번째 수까지를 보고 싶어 String.format 을 사용했다는 차이점 밖에 없습니다. double 을 보면 파이썬, 자바, 자바스크립트 모두 동일하게 소수를 표현하고 있고 0.3을 제대로 표현하지 못한다는 점을 볼 수 있습니다. 왜 이런일이 벌어진 걸까요?

왜 이런일이 벌어질까?

• 기본적으로 컴퓨터는 실수를 표현하기 위해서 두가지 표기법을 사용합니다.
  • 고정 소수점 표기법(Fixed point notation)
  • 부동 소수점 표기법(Floating point notation)
• 이 둘의 가장 큰 자이점은 소수점이 움직일 수 있는지 없는지로 판별할 수 있습니다.

고정 소수점 표기법

• 소수점이 고정되어 있는 실수 표현법입니다.
• 32비트 실수를 고정 소수점 방식으로 표현하면 다음처럼 표현할 수 있습니다.

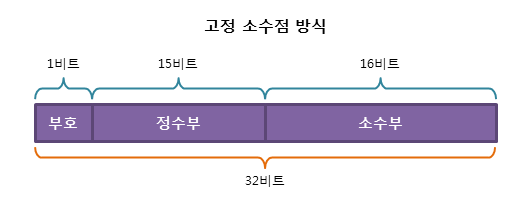
• 고정 소수점은 부호, 정수부, 소수부를 표현하는 3부분으로 나뉘고 크기가 고정되어 있습니다.
• 따라서 큰 수를 표현하거나 아주 작은 수를 표현하기에는 적합하지 않습니다.
• 예를 들어 7.75를 2진수로 변환해 본다면 아래의 그림처럼 표현 할 수 있습니다.(편의상 16비트 체계로 사용했습니다.)

• 

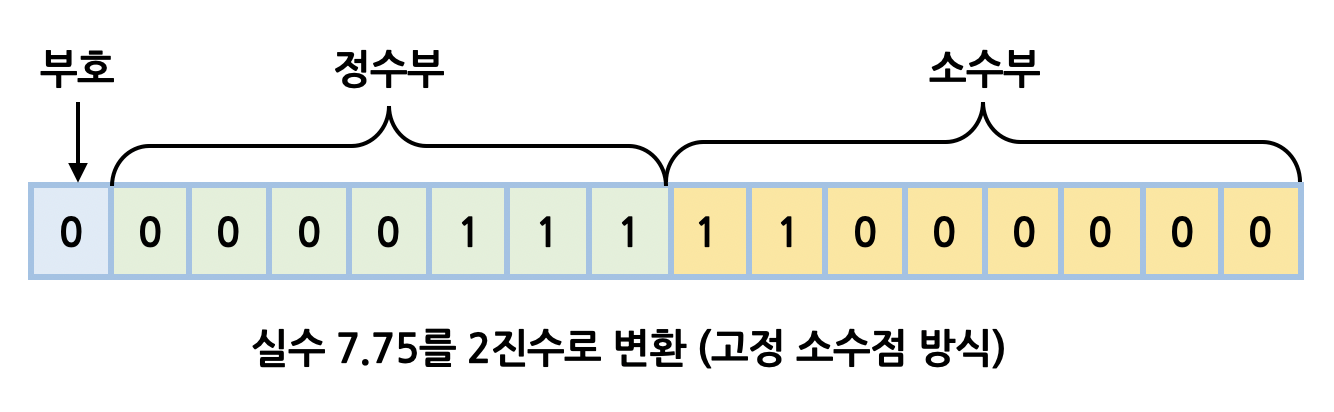
• 하지만 보기에도 만약 128 이상이면 어떻게 할까요? 또는 1/512을 표현하려면 어떻게 해야할까요? 해당 방법은 범위가 제한적이다라는 것을 알 수 있습니다.
• 따라서 잘 사용되지 않습니다.

부동 소수점 표기법

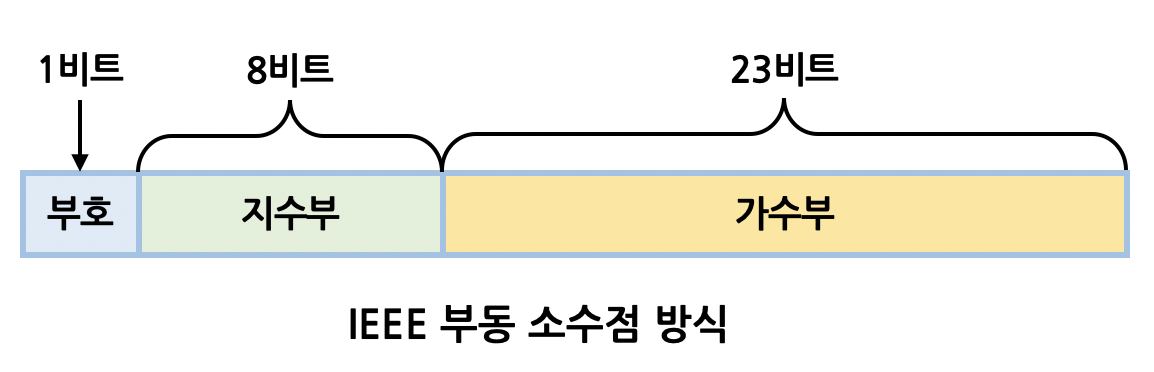
• 해당 방법은 실수를 부호부(sign), 가수부(Mantissa), 지수부(Exponent)로 나눕니다.
• 부동 소수점 변환기 를 사용하면 좀 더 편하게 이해하실 수 있습니다.
• 보통 언어에서 표현하는 실수 표현방법에 해당 방법이 사용됩니다. (Float, Double)
• 기본 수식으로는 (-1)^S x M x 2^(E)로 표현할 수 있고 각 역할은 다음과 같습니다.
  • S: 부호부(Sign) 1비트를 의미하며 0이면 양수고, 1이면 음수가 됩니다.
  • M: 가수부(Mantissa) 23비트를 의미하며, 양의 정수로 표현합니다.
  • E: 지수부(Exponent) 8비트를 의미하며, 소수점 위치를 나타냅니다.

  

• 만약 -12.34 를 부동 소수점 방식으로 표현해보면 아래와 같습니다.

• 

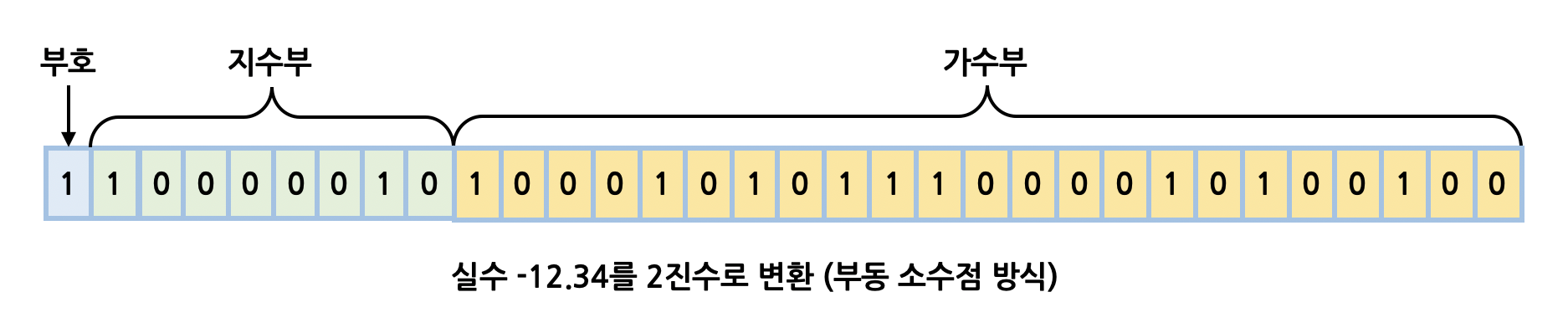
하지만 해당 방법도 표현할 수 있는 범위의 정확성에 한계가 있습니다.

어떻게 해결 할 수 있을까?

• 내부적으로 발생할 수 있는 작은 오차인 epsilon 값을 두어 해당 오차보다 아래인 경우 같다고 할 수 있습니다.
• 해결책은 자바의 경우 BigDecimal 을 사용하는 것이고 파이썬의 경우는 Decimal 모듈을 사용하는 것입니다.
  • 공식문서에 보면 int[], char[] 배열을 활용하여 자리 끼리 연산하는것을 볼 수 있습니다.
  • 이 방법을 arbitrary precision 이라고 합니다.
    • 자리수 단위로 쪼개어 배열형태로 표현합니다.
    • Overflow가 발생하지 않습니다.
    • 속도보단 정확성이 더 중요한 경우 사용됩니다.
    • 상당히 느립니다. 부동 소수점 표기법의 경우 하드웨어로 구현되는 반면 해당 기술은 소프트웨어로 구현해야 되기 때문입니다.
    • 돈, 로켓, 암호학등
    • 파이썬의 경우 버전 3 부터 long 타입이 없어졌습니다.
    • 파이썬 2의 경우 int 는 Fixed Precision 이었고 long은 arbitrary precision 정수였기 때문에 달랐지만 파이썬 3에서는 int 는 arbitrary precision 을 지원하고 fixed precision 은 더이상 지원되지 않습니다.

    import sys 
    ​
    a = sys.maxsize
    print(type(a))
    a = a+1
    print(type(a))
    ​
    # int
    # int