Insertion sort
Insertion Sort
shell sort의 Base가 되는 sort는 insertion sort 라고 할 수 있다. 또한 Insertion sort의 시간 복잡도는 O(N^2)이지만 selection sort와 bubble sort 보다 실제 sort를 돌려보면 위의 둘보다는 빠른 속도에 sort 가 되는 것을 알 수 있다.
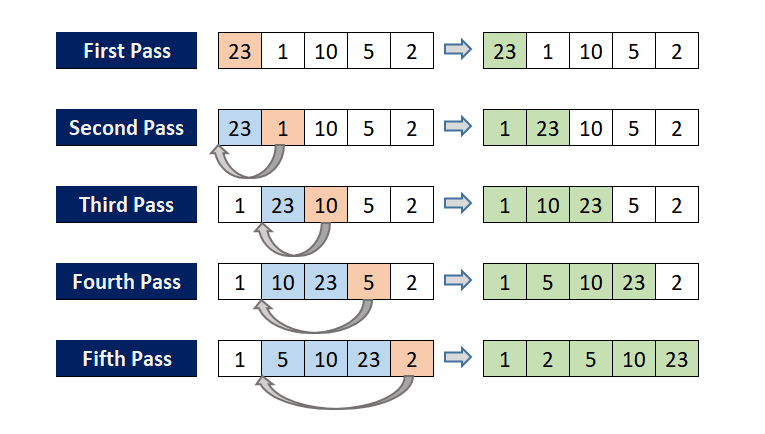
위의 그림과 같이 insertion sort는 시작인 index가 0인 원소는 이미 정렬되어 있다고 생각한다.
그다음 첫번째 부터 그 이전의 원소와 비교하면서 만약 자신보다 앞에 있는 원소가 크면 옮긴다. 그렇지 않으면 그대로 위치한다.
Second Pass를 보게 되면 1이 23보다 작기 때문에 앞으로 옮겨진것을 볼 수 있다.
Third pass를 보면 10은 23보다 작기 때문에 앞으로 또 옮겨진다. 이걸로 끝나는 것이 아니라 1과도 비교를 한다. 이때 1은 10보다 작기때문에 그대로 10은 2번째 index에 위치한것을 볼 수 있다.
이를 기반하여 코드를 확인해보면
def insertion_sort(arr):
for end in range(1, len(arr)):
for i in range(end, 0, -1):
if arr[i - 1] > arr[i]:
arr[i - 1], arr[i] = arr[i], arr[i - 1]첫번째 for 함수가 1부터 시작하는 것을 볼 수 있다. 0번째 index 는 이미 정렬되어 있다고 생각하는 것이다.
두번째 for 함수부터는 처음 고시한 i 부터 0 까지 -1씩 움직이는 것을 볼 수 있다. (참고로 for i in range(end , 0 ,-1) 은 range(시작, 끝, 얼만큼씩 이동할 것인지) 를 나타낸다. )
그리고 만약 비교 기준과 기준보다 앞에 있는 원소와 비교하여 더 작으면 바꾼다. (arr[i - 1], arr[i] = arr[i], arr[i - 1]와 같이 파이썬은 tmp 같은거는 쓰지 않아도 SWAP 이 가능하다.)
더 최적화를 해보면
def insertionsort(MyList):
for i in range(len(MyList)):
curr = MyList[i]
j = i-1
while j >= 0 and curr < MyList[j] :
MyList[j + 1] = MyList[j]
MyList[j] = curr
j = j - 1위와 같은 코드로 나타낼 수 있다.
처음 코드와 같이 실제로 while 이 돌아가는것은 i가 1부터인것을 알 수 있다. 처음 코드와 다른 점은 위의 while 조건문에 curr < MyList[j]의 조건문이 하나 있는 것을 알 수 있는데 바로 여기서 curr 이 MyList[j] 보다 작은 수를 만나면 더 앞으로 가면 안되고 바로 그 점이 curr이 위치할 index 이므로 while 문을 나가게 된다.